The hydraulic power, PHyd, required to move a body of
water frictionless from one elevation to another at a given flow
rate is

|
(4) |
The hydraulic efficiency, e, can be determined by
combining Equations 2 and 4.
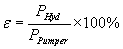
|
(5) |
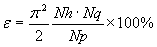
|
(6) |
It has been shown that there is a direct relationship between e, the droplet size distribution, and the entrainment of organic in
aqueous and aqueous in organic. The higher the efficiency the larger the droplets and the lower the entrainment [3-6]. The hydraulic efficiencies of Examples 1-5 are 16.9%, 16.3%, 20.8%, 20.0%, and 17.1%, respectively. None of these efficiencies are stellar, but Example 3 would give the best
results. The R320 group of curved bladed pumpers achieve efficiencies of 30-40% and these have been responsible for organic in aqueous entrainments between 1-10 ppm and 25-50 ppm aqueous in
organic [5]. It is therefore advisable to try and design an SX-circuit around the pumperís maximum
efficiency. Figure 6 shows the hydraulic efficiency as a function of Nq and DO/D for the R300.
Figure 6:Hydraulic efficiency of the straight-bladed
R300 as a function on Nq and DO/D.
Examples 1-5 used DO/D=0.33 and most of the examples were operating near peak
efficiency. For Nq=0.1, the peak efficiency is achieved with an orifice ratio, DO/D=0.37-0.5.
For Nq < 0.175, DO/D=0.46 always gives the maximum efficiency. In general an orifice ratio,
DO/D=0.5 gives the best results. For Nq > 0.175, the orifice should be made larger. Figure 6 even
shows that if the design would call for a flow number, Nq > 0.24, the orifice should be the
same diameter as the pumper.
In order to improve on Example 5, the orifice could be cut out to a DO/D range of 0.37-0.5. The hydraulic efficiency would increase to at least 26%, meaning that the
power to drive the pumper would be much smaller at the same head and flow (not
the same Nh and Nq).
Hydraulic efficiencies of other pumpers have been published [2-6]. They all behave in a similar fashion. The impeller design that achieves the lowest consumed power and the highest head for a given flow rate
is the most efficient pump mixer. It is important to choose the orifice size that optimizes the
efficiency. In general the order of impellers from highest efficiency to lowest is:
To
make an exact comparison, the power-flow and head-flow curves of the pumpers are
needed. Lightnin has these for over 300 pumper designs [2]. They can also be determined
experimentally (described previously).
When
designing a new SX plant it is important to design the pumpers so that they are
on the left hand side of the efficiency optimum (Figure 6). Once the decision is made to increase production, the only way to do so with the existing equipment is to increase the pumper speed. The operating point will move to the right. By starting at the left of the maximum, an increase in speed
will keep the hydraulic efficiency high with similar entrainment.
Operating Ranges
A successful SX pumper stage should not have air entrainment nor have phase separation. Air entrainment causes a lot of problems in the settlers, where aqueous droplets cling to small gas bubbles and float
in the organic layer. Air is also a component of crud. Air is entrained when too much mixing energy is
in the pump box. The surface is wild and the vortexing can be seen and heard. The upper level of the power dissipation range, PAir/V, depends on mean residence time, q Res and Z/T ratio.
An approximate correlation is:
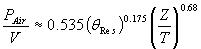 |
(7) |
where P/V is in kW/m3, q Res is in seconds, and Z/T is dimensionless. Assuming a 40 second residence time and Z/T=0.8, PAir/V=0.88 kW/m3 (4.38 Hp/1000 gallons). A 5 second residence time and Z/T=0.215 results in only PAir/V=0.25
kW/m3 (1.25 Hp/1000 gallons).
Notice that a reduction in Z/T reduces PAir/V. This means that air induction is more
likely at lower aspect ratios. Several older plants and the Outokumpu DOP have very small Z/T,
and operate above PAir/V. Davy was innovative and designed an egg crate to minimize vortexing. Outokumpu uses an air shield to minimize splashing and vortexing [8]. If it is unavoidable to run the pumper below PAir/V, a solution like one of these is necessary.
Too little power is just as bad. Phase separation can cause many problems, including less mass
transfer and increased head requirements. The lower level of the power dissipation range, PPS/V, depends on mean residence time, qRes and Z/T ratio, too. An
approximate correlation is:
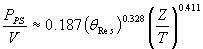 |
(8) |
Assuming a 40 second residence time and Z/T=0.8, PAir/V=0.57 kW/m3 (2.86 Hp/1000 gallons). A 5 second residence time and Z/T=0.215 results in only PAir/V=0.17 kW/m3 (0.84 Hp/1000 gallons).
Tight as these ranges are, it is important to try and stay within these ranges for an optimized SX pumper stage.
Pilot Plants Look Different
|
